LES CIRCUITS DES OSCILLATEURS
1-Les critères d'oscillations de Barkhausen
1.1. Schéma bloc :
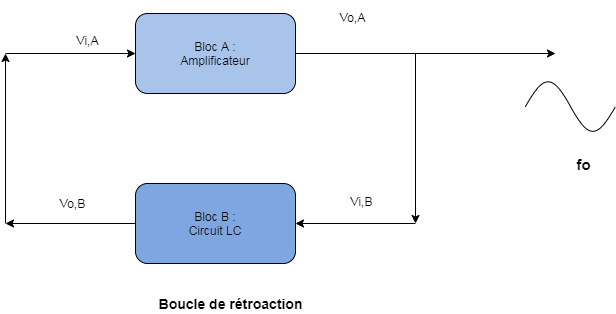
Un circuit oscillateur est composé de deux blocs :
- Le bloc [A] désigne le bloc amplificateur ayant un gain en tension Av = (VoA / ViA) et un déphasage
φA entre les 2 tensions d'entrée et de sortie ;
- Le bloc [B] désigne le bloc résonant LC ayant un gain en tension Bv VoB / ViB) et un déphasage
φB entre les 2 tensions d'entrée et de sortie du bloc B.
La relation entre les deux blocs lorsque les oscillations sont produites est donnée par l'ensemble des relations suivantes :
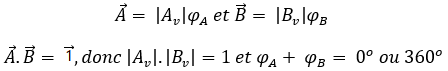
En d'autres mots si le bloc A amplifie la tension le bloc B doit l'atténuer dans la même proportion. Similairement, si le bloc A créé un déphasage
le bloc B le corrigera pour le remettre à 0 ou 360o.

2-L'émetteur en commun
2.1. Circuit :
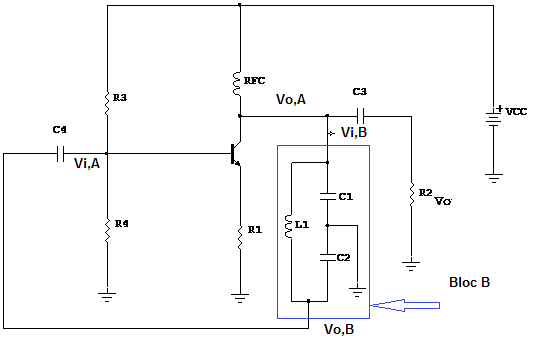
La fréquence d’oscillation du circuit fo est égale à la fréquence de résonance du circuit du bloc B :
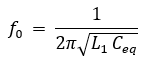 avec Ceq = C1 en série avec C2.
Le gain du bloc B, Bv est : Bv = Vo,B/Vi,B = -(C1/C2)
avec Ceq = C1 en série avec C2.
Le gain du bloc B, Bv est : Bv = Vo,B/Vi,B = -(C1/C2)
2.2. Rôle de la bobine RFC : Le rôle de la bobine RFC 'Radio Frequency Choke' est d’empêcher les oscillations de revenir
sur la ligne d’alimentation du circuit oscillateur. Sa valeur suggérée est de 10 fois l’inductance L1 utilisée dans le bloc B du circuit
oscillateur. Cependant la résistance de ses enroulements permet l’alimentation du transistor du bloc A.

3- Le collecteur en commun
3.1 Circuit :
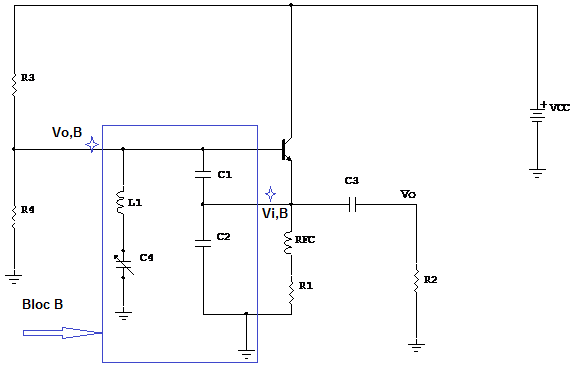
La fréquence d’oscillation du circuit fo est égale à celle du circuit de l'émetteur en commun sauf que Ceq = C1 en série avec
C2 en série avec C4 . Le condensateur C4 est variable et est utilisé pour varier la fréquence d'oscillation fo.
Le gain du bloc B est :
Bv = Vo,B/Vi,B = 1 + (C2/C1). Les caractéristiques de
l’inductance RFC du collecteur en commun sont identiques à celles de l’émetteur en commun vu dans le paragraphe précèdent.

4- La base en commun
4.1 Circuit :
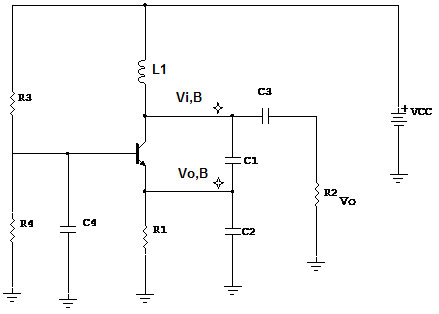
La fréquence d’oscillation du circuit fo est égale à celle du circuit de l'émetteur en commun avec Ceq = C1 en
série avec C2. Le gain du bloc B est :
Bv = Vo,B/Vi,B = C1 / (C1 + C2) .
4.2 Caractéristiques du circuit de l’oscillateur base en commun :
On note l’absence de la bobine RFC du circuit oscillateur. En pratique la bobine du bloc B joue les 2 rôles, celui de la RFC et celui de la
bobine du circuit résonant LC. Un avantage économique sur les circuits des 2 oscillateurs vus avant.
5- Comparaison des trois circuits oscillateurs :
La question qui se pose : Lequel des trois circuits peut produire la plus grande fréquence d’oscillation ? La réponse est dictée principalement
par le UGB du circuit bu bloc A. On rappelle que le UGB ‘Unity Gain Bandwidth product’ limite la fréquence de fonctionnement
d’un circuit amplificateur. La relation est UGB = f × AV du circuit, sachant que le UGB est fixe alors si AV ↑
⇔ f ↓. Parmi les 3 oscillateurs on note que la partie amplificateur du collecteur en commun a un AV ≼ 1 donc sa fréquence
d’opération serait la plus grande des 2 autres circuits.
Maintenant entre l’émetteur en commun et la base en commun il faut regarder lequel des 2 circuits offre le moins d’effet parasite en haute
fréquence. On rappelle l’effet parasite capacitif totale vu à l’entrée d’un circuit amplificateur est CT,i = Cbe + CMiller
avec CMiller = (1-AV). Sachant qu’on ne peut pas considérer le Cbe dans le cas de la base en commun alors
l’effet parasite total de ce circuit est légèrement inférieur à celui de l’émetteur en commun ce qui nous amène à dire que pour le même gain
AV le circuit de la base en commun peut monter plus en fréquence que celui de l’émetteur en commun. La table ci-dessous résume l'analyse
de la réponse en fréquence des circuits oscillateurs.

| Émetteur en commun | Collecteur en commun | Base en commun | |
|---|---|---|---|
| fréquence f0 | Basse | Haute | Moyenne |
| Impédance d'entrée Zi | Haute | Haute | Basse |
| Impédance de sortie Zo | Haute | Basse | Haute |